
Das doch recht seltsame Geschäftsmodell des Osterhasen sieht vor, Ostereier, Süßigkeit und Schokolade an den unterschiedlichsten Orten zu verstecken. Das eigentliche Ziel ist dabei aber nicht, diese Kostbarkeiten sicher vor fremdem Zugriff zu schützen, sondern vielmehr das Gegenteil, nämlich, dass sie gefunden werden (deshalb auch Ostereiersuche). Ein zu gut verstecktes Osternest bereitet früher oder später eher weniger Freude.
Das Spiel zwischen uns, den Suchenden, und dem Osterhasen besteht somit darin, dass wir genau dort suchen, wo das Geschenk auch versteckt ist. Damit liegt im Grundsatz ein Koordinationsproblem vor: An welchem Ort treffen sich die Suchenden und der Verstecker?
Wir können die Eiersuche als Spiel darstellen: Unter einem Spiel wird in der Spieltheorie eine strategische Interaktion zwischen mehreren Entscheidern („Spielern“) verstanden. Die aus der Mathematik stammende Spieltheorie ist eine Methode, die mittlerweile grundlegend für sämtliche Bereiche der Wirtschaftswissenschaften geworden ist (Bartholomae 2022). Die Ostereiersuche kann in der Struktur des „Kampfs der Geschlechter“ (Bartholomae/Wiens 2020, 104f), einem spieltheoretischen Archetyp, beschrieben werden.
Es gibt zwei Spieler: Uns, die wir suchen, und den Osterhasen, der die Geschenke versteckt. Beide können einen Ort wählen, an dem sie suchen bzw. verstecken. Gehen wir zur Vereinfachung davon aus, dass es nur zwei Möglichkeiten gibt: Ein Versteck im Haus oder im Garten. Nehmen wir ferner an, dass sowohl der Osterhase als auch wir bestimmte Vorlieben haben: Während wir lieber im Haus suchen, da wir uns dort besser zurechtfinden, bevorzugt es der Osterhase, die Geschenke im Garten zu verstecken, da er nur ungern sein gewohntes Terrain verlassen möchte. Diese Präferenzen werden im in der Abbildung dargestellten Spiel dadurch ausgedrückt, dass dem bevorzugten Versteck ein höherer Nutzen (3) als dem anderen Versteck (1) zugewiesen wird. Dennoch wollen wir und der Osterhase, dass die Geschenke gefunden werden, weshalb eine Fehlkoordination, z. B., wenn wir im Haus suchen und die Geschenke im Garten versteckt sind, von allen mit einem Nutzen von 0 quittiert wird.
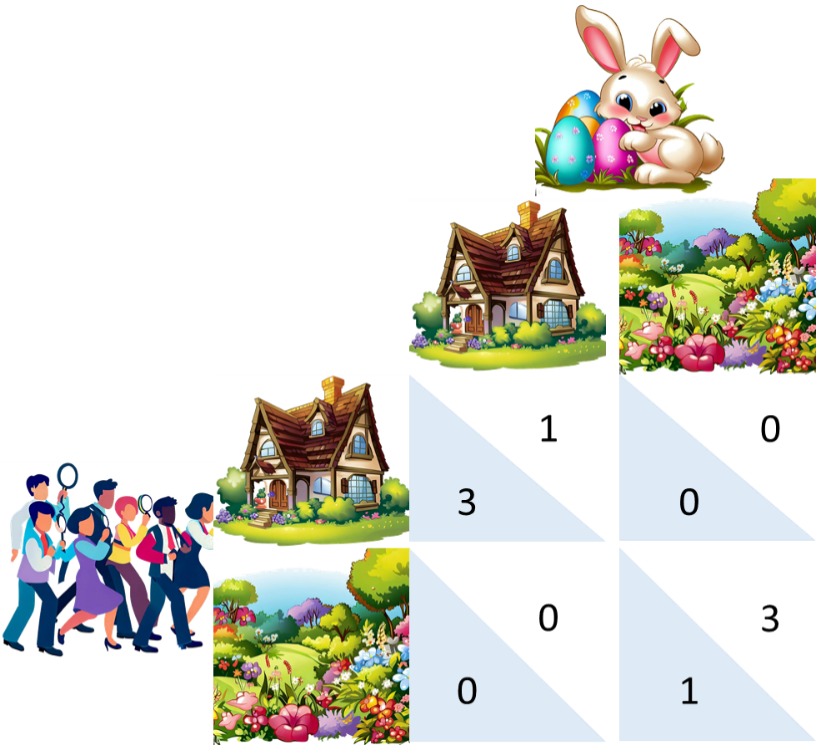
Wir können leicht erkennen, dass es zwei Gleichgewichte gibt, die sich dadurch auszeichnen, dass sich keiner besserstellen kann: Versteckt der Osterhase das Geschenk im Haus, ist es am besten, wenn wir im Haus suchen; suchen wir im Haus, möchte der Osterhase es auch dort versteckt wissen. Gleiches gilt für die Suche bzw. das Versteck im Garten. Der Unterschied zwischen beiden Gleichgewichten besteht darin, dass entweder der Osterhase oder wir dieses bevorzugen.
Allerdings besteht ein Koordinationsproblem: Welches der beiden Gleichgewichte wird sich einstellen? Schließlich sind beide gleichermaßen plausibel. Damit besteht die Gefahr, dass wir etwa im Haus suchen, da wir dieses Gleichgewicht vermuten, der Osterhase aber tatsächlich den Garten gewählt hat. Das Problem löst sich, wenn einer der beiden Spieler beobachtbar vor dem anderen eine Entscheidung treffen kann: Also, wenn wir beobachten können, dass der Osterhase in den Garten oder in das Haus hoppelt. Dabei ist klar, dass der Zuerstziehende („first mover“) einen Vorteil hat und den bevorzugten Ort wählen wird. Der Osterhase würde folglich sicherlich in den Garten hoppeln, der sein bevorzugter Ort ist.
Das Problem bleibt aber bestehen, wenn weder wir noch der Osterhase beobachten können, wie der jeweils andere entscheidet. Hier kann ein Fokuspunkt (Bartholomae/Wiens 2020, 104) weiterhelfen: Das kann zum einen ein Gleichgewicht sein, das für beide attraktiver ist, da es beispielsweise eine höhere Gesamtauszahlung ermöglicht. Ein solches liegt hier leider nicht vor, da in beiden Gleichgewichten die Summe gleich hoch ist. Zum anderen kann sich aber auch ein Fokuspunkt von außerhalb der eigentlichen Spielsituation ergeben. So könnte es etwa Tradition sein, dass das Nest bei der Ostereiersuche immer im Garten versteckt wird. Besteht die Möglichkeit einer vorangegangenen Kommunikation, kann auch ein gemeinsamer Zufallsmechanismus mit korrelierten Wahrscheinlichkeiten für die Strategiewahl genutzt werden. Konkret heißt dies, dass die Strategiewahl z. B. in Abhängigkeit eines Zufallsereignisses wie dem Wetter erfolgt: Bei schönem Wetter wird das Nest im Garten versteckt und gesucht und bei Regen entsprechend im Haus.
Im Wirtschaftskontext gibt es viele weitere Beispiele für solche Koordinationsprobleme, wie etwa die Einigung von Unternehmen auf einen gemeinsamen Standard. Somit hilft uns der Osterhase erneut, uns auf weitere Herausforderungen vorzubereiten. In diesem Sinne: Viel Erfolg beim Suchen und frohe Ostern!
Literatur:
- Bartholomae, F. W. (2022): Aus der Spieltheorie für die Praxis lernen, people&work, 3/2022, 26-30.
- Bartholomae, F. W.; Wiens, M. (2020), Spieltheorie – Ein anwendungsorientiertes Lehrbuch, 2., aktual. u. erw. Aufl., Springer Gabler: Wiesbaden.
Für Inhalt und Form dieses Beitrags ist der Autor verantwortlich.




