
The quite strange business model of the Easter Bunny involves hiding Easter eggs, candy, and chocolate in many different places. However, the primary goal is not to protect these treasures from unauthorized access, but rather the opposite, that is, to ensure that they are found. An Easter nest that is too well hidden tends to bring less joy sooner or later.
The game between us, the searchers, and the Easter bunny is therefore to search exactly where the gift is hidden. Consequently, we face a coordination problem on principle: At which place do the searchers and the hider meet?
The search for Easter eggs can be illustrated as a game. In game theory, a game is a strategic interaction between several decision-makers (“players”). Originating in mathematics, game theory is a method that has now become fundamental to all areas of business and economics (Bartholomae 2022). The search for Easter eggs can be described using the structure of the “battle of the sexes” (Bartholomae/Wiens 2020, 104f), a game-theoretical archetype.
There are two players, us who search, and the Easter bunny who hides the gifts. Both can choose a place to search or hide. For simplicity, let us assume that there are only two possibilities: A hiding place in the house or in the garden. Let us further assume that both the Easter Bunny and we, have certain preferences: While we prefer to search in the house since we are more comfortable there, the Easter Bunny prefers to hide the gifts in the garden since he is reluctant to leave his familiar terrain. These preferences are expressed in the game shown in the figure by assigning a higher utility (3) to the preferred hiding place than to the other hiding place (1). Nevertheless, we and the Easter Bunny want the gifts to be found, consequently a miscoordination, e.g., if we search in the house and the gifts are hidden in the garden, would be reflected in a utility of 0 for both.
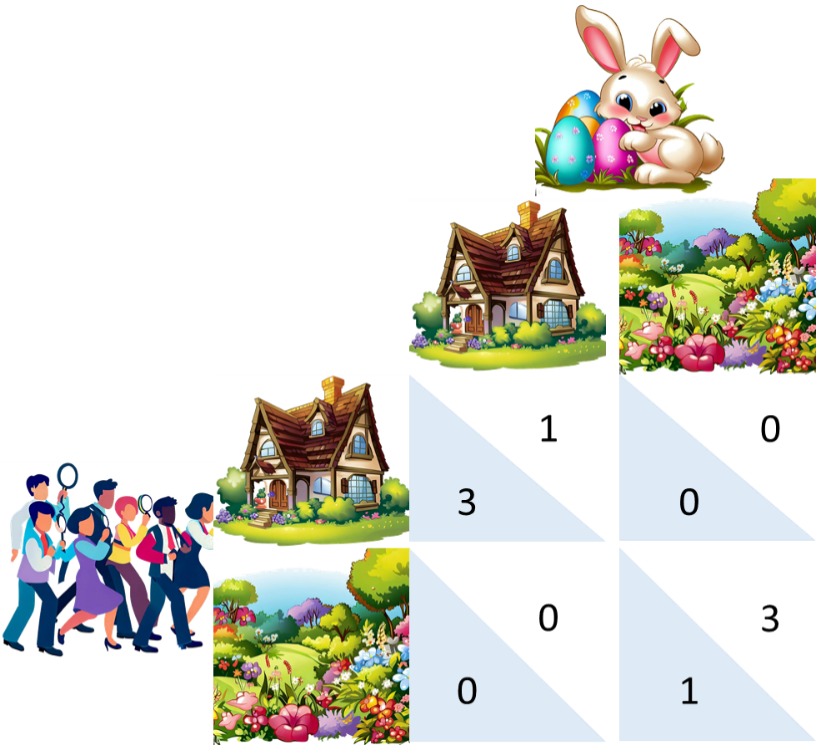
It is easy to see that there are two equilibria, characterized by the fact that no one can do better: If the Easter bunny hides the gift in the house, it is best if we look in the house; if we look in the house, the Easter bunny wants it hidden there as well. The same applies to the search or hiding in the garden. The difference between the two equilibria is that either the Easter Bunny or we prefer them.
However, there is a coordination problem: Which of the two equilibria will result? After all, both are equally plausible. Thus, there is the possibility that we search in the house, for example, because we assume this equilibrium, but the Easter bunny has actually chosen the garden. The problem is solved if one of the two players can observably decide before the other: That is if we can observe that the Easter bunny hobbles into the garden or the house. Obviously, the first mover has an advantage and will choose the preferred location. Consequently, the Easter bunny would certainly hobble into the garden, his favorite spot.
The problem remains, however, if neither we nor the Easter bunny can observe how the other decides. In this case, an orientation or focus point (Bartholomae/Wiens 2020, 104) can help: On the one hand, this can be an equilibrium that is more attractive for both, since it allows for a higher total payoff, for example. Unfortunately, such an equilibrium is not present here, since the total is the same in both equilibria. On the other hand, a focus point can also result from outside the actual game situation. For example, it could be a tradition that the nest is always hidden in the garden. If there is the possibility of prior communication, a joint random mechanism with correlated probabilities can also be used for strategy selection. Specifically, this means that the strategy choice is made, for example, depending on a random event such as the weather: If the weather is sunny, the nest is hidden and searched for in the garden, and if it rains, accordingly, in the house.
In the business and economic context, there are many other examples of such coordination problems, such as companies agreeing on a common standard. Thus, the Easter Bunny helps us once again to prepare for further challenges. In this sense: Good luck with the search and Happy Easter!
The author is responsible for the content and form of this article.




